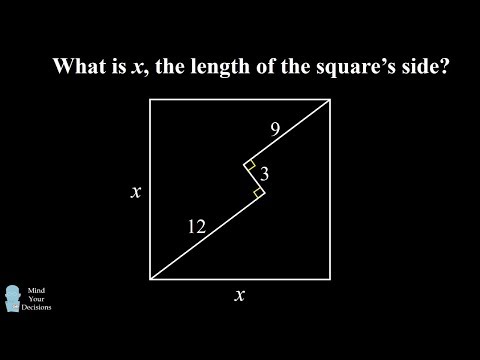Can Form 2220 Respectively 2023-2024

Hey, this is Pressure Locker. We'll start out with this square. From the bottom left corner of the square, I'll draw a line segment to the interior with a length of 12. From the endpoint of this line segment, I'll construct a perpendicular going up and to the left with a length of 3. From the endpoint of this line segment, I'll construct another perpendicular that connects to the upper right-hand corner of the square. This line segment has a length of dyeing. The question is, from the given information, what is X? The length of the square's side. Can you figure it out? Give this problem a try, and when you're ready, keep watching the video for the solution. So before I present the approach that eventually led me to the answer, I want to go over some of the approaches that did not work for me. I first considered the right triangles in the interior of the square. While I could solve for the areas of these triangles and the hypotenuse of these triangles, this didn't lead me directly to the length of the square side. I then tried to work out the problem using coordinate geometry, but in spite of trying a few equations, I still wasn't able to solve for X. So then it struck me, in the third approach I took to this problem, I imagined focusing on just the inside line segments in the interior of the square. I wanted to figure out the distance from end to end, so I considered what would happen if I rotated the figure so it'd be easier to analyze. Then it struck me, I connected the endpoints of these line segments, and then I realized we basically have one large right triangle. I can move the length of nine...