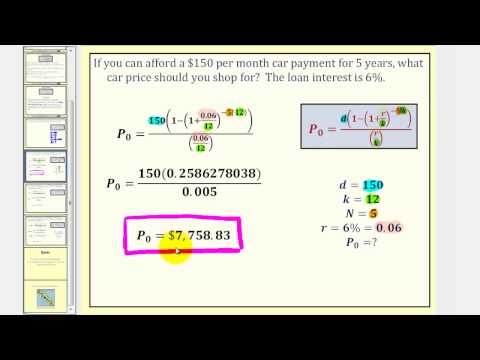
Welcome to a lesson on the loan formula. This lesson is about conventional loans, also called amortized loans or installment loans. Examples include auto loans and home mortgages. The techniques in this lesson do not apply to payday loans, add-on loans, or other loan types where the interest is calculated upfront. Though I do have lessons on these topics. One great thing about loans is that we can use the same formula as a payout annuity. To see why, imagine that you had $10,000 invested at a bank. You start taking out withdrawals while earning interest on the remaining balance as part of a payout annuity. After five years, your balance is zero. Flip that around and imagine that you borrow $10,000 from a bank. You make payments back to the bank with interest for the money you borrow. After five years, the loan is paid off. The roles are reversed, but the formula to describe the situation is the same. So here is the loan formula, which again is the same as the payout annuity formula: P Sub Zero is the loan amount or beginning balance or principal. D is the loan payment or the payment per unit of time. R is the annual interest rate expressed as a decimal. K is the number of compounding periods in one year. Notice K appears three times in the formula. N is the length of the loan in years. Now, the compounding frequency is not always explicitly given but can be determined by how often payments are made. Before we take a look at two examples, though, it is important to be very careful about rounding when calculations involve exponents. In general, keep as many decimals during calculations as you can. Be sure to keep at least three significant digits, meaning three numbers after any leading zeroes. For example, to round...
Award-winning PDF software





Video instructions and help with filling out and completing Form 2220 Installment