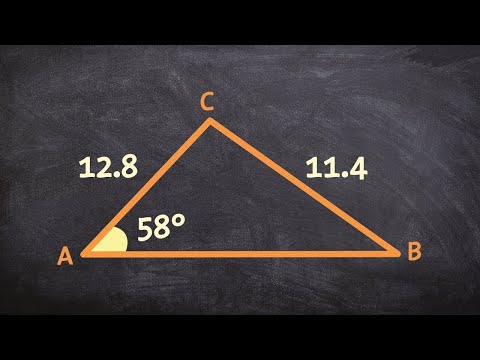
Okay, so right now, ladies and gentlemen, we have the following information: B = 12.8 and A = 11.4. Let's draw the triangle and label the angles and sides accordingly. We know that A is 58 degrees and C is unknown. We can see that we have a side-side-angle relationship, which means there are multiple possibilities for the triangle. We can have two different triangles with one possibility being AOB and the other being AOC. We can also consider the possibility of C not touching the given sides, resulting in no triangle. To find the missing angle C, we can use the law of sines. Setting up the equation, we have 11.4/sin(58) = 12.8/sin(B). Simplifying this equation, we get sin(B) = (12.8*sin(58))/11.4. Solving for B, we can calculate sin(B) and find B to be 72.21 degrees. However, when dealing with inverse sine, we need to consider the two possible values. For example, when sin(B) = 1/2, the possible values for B are pi/6 and 5pi/6. Therefore, we have two possible values for angle B.
Award-winning PDF software





Video instructions and help with filling out and completing Form 2220 Solutions